ブラウザ上で画像処理 ~漫画のコマを領域分割する~

はじめに
こんにちは、pixiv でアルバイトをしていた arayuji です。
今回はこれまでやってきたことのまとめとして、漫画やイラストに対する画像処理についてご紹介します。
一口に画像処理といっても様々なものがありますが、ここでは漫画のコマや白黒のイラストを簡単に領域分割する手法についてお話しします。 基本的な画像処理から高度な最適化処理まで、すべての処理をブラウザ上で 実現しました。
実際のコードも、pixiv/manga-segment · GitHubにあるので、興味がある方は見てみてください。
デモ
トップに載せた画像が動作イメージなのですが、わかりにくいと思うのでデモを用意しました。(Chrome 40 / Firefox 35 / IE 11 で動作確認しましたが、IE では非常に遅いので注意してください)
右側のパレットで色をひとつ選んで、左側の画像の上にマウスで線を描いてみてください。描いた線に応じて領域分割された結果が表示されます。
画像処理?
そもそも、画像処理はどのようなものでしょうか。
- 写真の補正
- カメラで顔を認識してくれる機能
- 似ている画像を検索するサービス
などが身近かと思います。
実は技術的にも、色を調整するような簡単なものから、高度な処理を行うものまで、様々あります。
- 色の反転・調整
- ぼかしや鮮鋭化などのフィルター
などが基本的なものとして挙げられます。 これらは身近な例でいえば写真の補正などに応用され、Photoshop など画像編集ソフトなどでも手軽に使えるようになっています。
もう少し高度な処理をするものには、
- 顔検出(下図。©OpenCV)
- 類似画像検索
などです。 この辺りも、カメラで笑顔の瞬間を撮影する機能が搭載されたり、Google で似ている画像を検索できるようになるなど、身近になってきています。

最近はさらに研究が進み、
- 3次元映像の処理
- 一般の物体認識
なども実現されつつあります。これらも Kinnect といった商用化の例もありますが、まだまだ手軽に使えるといった状況にはありません。
そこで、今回はこのような最新の画像処理を手軽に使える形で実装してみることにしました。 pixiv でもよく投稿される漫画の画像を対象に、ユーザーが簡単に描いた線で領域分割する処理を、ブラウザ上で動くようにしました。
理論
まずは、どのような理論に基づいて領域分割を行っているのかについて説明しておきます。
全体の流れ
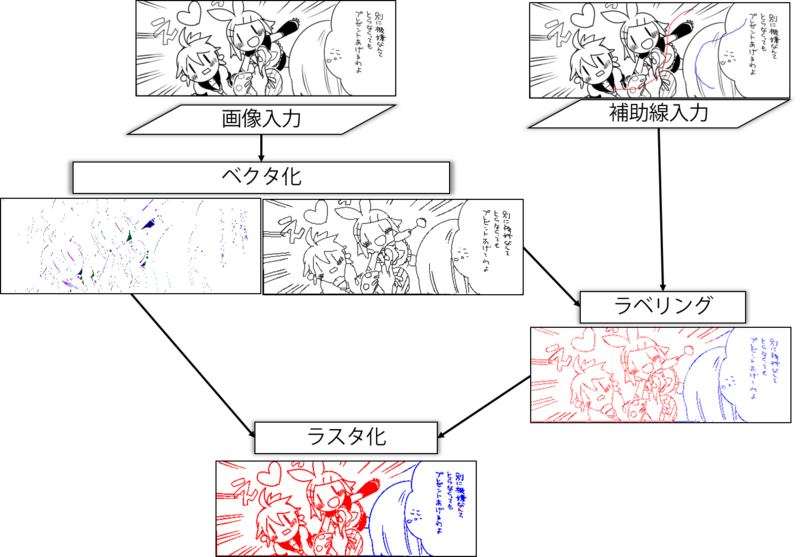
流れを簡単にまとめると、このようになります。
- 入力された「漫画のコマの画像」を、「ベクタ画像」+「方向マップ」に変換します。
- この「ベクタ画像」と「ユーザーの描いた線」との間の類似性から、最適な色の割り当て方を求めます。
- この割り当て方と「方向マップ」を使って、ユーザーの描いた線→ベクタ画像→元の画像全体へと、順に色を伝搬させます。
以下で順に説明していきます。
ベクタ画像+方向マップへの変換
漫画のコマの画像は、たくさんの色(画素)が縦横に並んだ行列である「ラスタ形式」になっています。 まずは、これを「ベクタ画像」と呼ばれる画像に変換すること(ベクタ化)で、この後の処理ができる形式にします。 ベクタ画像というのは、始点と終点があるベクトルで表現した形式の画像のことです。 ベクタ化をしておくことで、線の方向の情報を使って処理が行えるようになります。

また、最後にラスタ形式に戻す必要があるのですが、この時に「方向マップ」というものが必要になるので、ここで同時に作成しておきます。 方向マップは、ベクタ化するときに失われてしまう線の幅の情報を保存しておく行列です。 ベクタ化の一部として線を細くする操作があるので、この操作を記録しておくイメージです。

上の図は方向マップを可視化したものですが、元の画像で黒く塗りつぶされていた部分に値が見られます。 これは、塗りつぶされた部分はベクタ化する過程で多くの情報が失われてしまうためです。
色の割り当て
前の処理から「漫画のコマのベクタ画像」が得られます。 実は、「ユーザーの描いた線」も、どこからどこまで線を引いたかという始点と終点の情報で表されるので、「ユーザーの描いた線のベクタ画像」といえます。 ユーザーが描いた線には色が付いているので、この「ユーザーの描いた線のベクタ画像」の色を「漫画のコマのベクタ画像」に割り当てればいいのです。
では、どのように色を割り当てればいいのでしょうか?
すぐ隣にあるなど似ているベクトルに別の色が付いてしまうと、同じ線の中でもまだら模様になってしまい、適切な割り当て方とは言えません。 そこで、似ている(距離が近く同じ方向を向いている)ベクトルには同じ色を割り当てる、というのを基本方針とします。 こうすることで、色が飛び飛びにならず、連続性のある割り当て方になります。
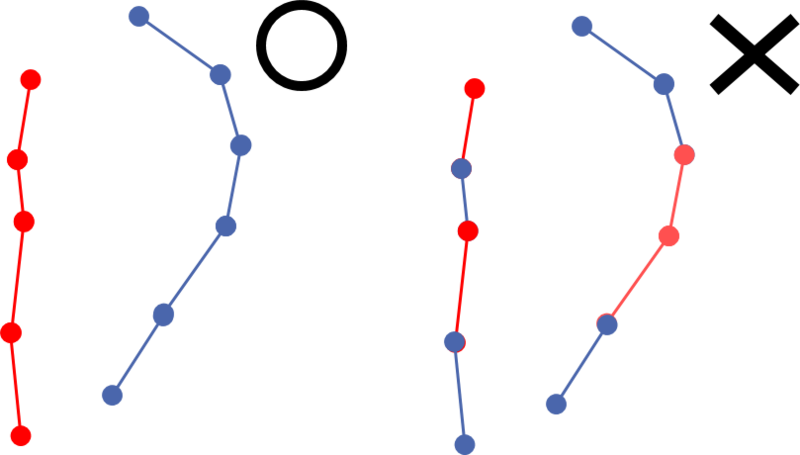
この方針は、大きく二つに分けることができます。
- 「漫画のコマのベクタ画像」の中の他のベクトルと似ているなら、その色を割り当てる
- 「ユーザーの描いた線のベクタ画像」の中のベクトルと似ているなら、その色を割り当てる
一つ目の条件を最大限優先すると、コマ全体を同じ色にするのが最適になります。 しかし、二つ目の条件を最大限優先すると、コマの中では色がばらばらになってしまいます。 つまり、この二つの条件はトレードオフの関係になっています。
そこで、色の割り当て方を以下のような一つの式(エネルギー関数)に落とし込み、計算によって最も望ましい解を求めることにします。
この関数の2つの項は、それぞれ先ほどあげた二つの条件に対応していて、ベクトル同士の距離と方向の類似性を表しています。 各項を小さくするほどその条件を優先することになり、色の割り当て方 Φ を変えてこの式全体を小さくすることが目標になります。 先ほどのトレードオフは、第1項と第2項は同時に小さくすることはできないという形で現れ、そのバランスが最適な場合を求めることになります。
そのために、この関数をさらにグラフ理論の問題に変換します。 例えば、ユーザーが赤と青の線を描いたとき、グラフは下の図のようになります。
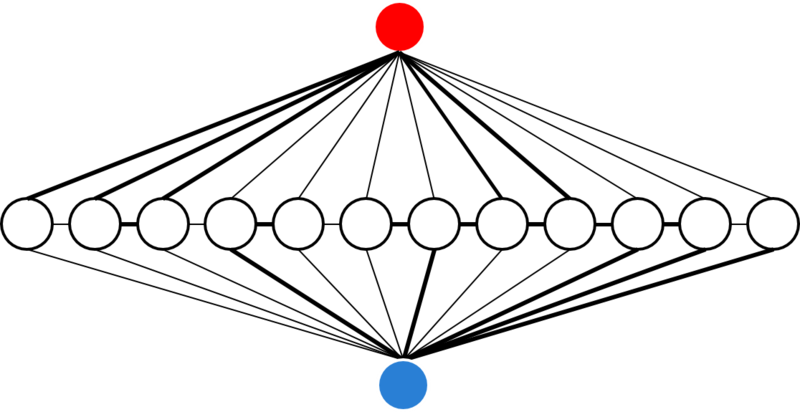
中央に横に並んでいるノードが画像内のベクトルに、上下の赤と青のノードがユーザーが描いた線にそれぞれ対応します。 中央のノード同士を結ぶエッジは、先ほどの式の第1項の値が重みになっています。 上下のノードと中央のノードを結ぶエッジは、第2項の値が重みになっています。
このグラフを下のように切断し、上に含まれるノードは赤、下に含まれるノードは青に割り当てるとします。 このとき、先ほどの関数を最小化することは、切断するエッジの重みの和を最小にすること(最小カット)に対応します。
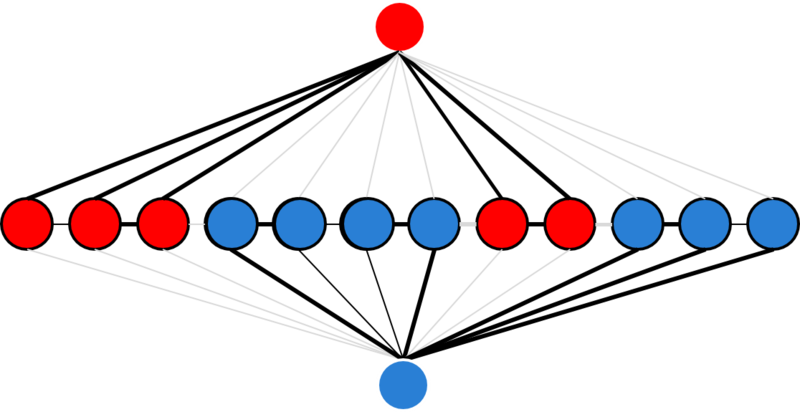
この最小カット問題は、様々な解法が知られているので、そのアルゴリズムを用いることで最適な切断を求めることができます。
色の伝搬
こうして色の割り当て方が決まれば、「ユーザーの描いた線」ヵら「漫画のコマのベクタ画像」に色を伝搬させることができます。

ただ、これではまだ細い線に色が割り当てられただけです。 この画像からさらに、元の画像全体に色を伝搬させる必要があります。 このために、ベクタ化の際に同時に作成した方向マップを使用します。
先ほども述べたとおり、方向マップには線を細くしたときの収縮の仕方が保存されています。 これを逆方向に辿っていくことで、元の太さの線を復元することができます。

この方向マップで行っている処理について、簡単な例を使って説明します。 下のような縦横それぞれ5画素の画像に対し、細線画像と方向マップを作成してあるものとします。
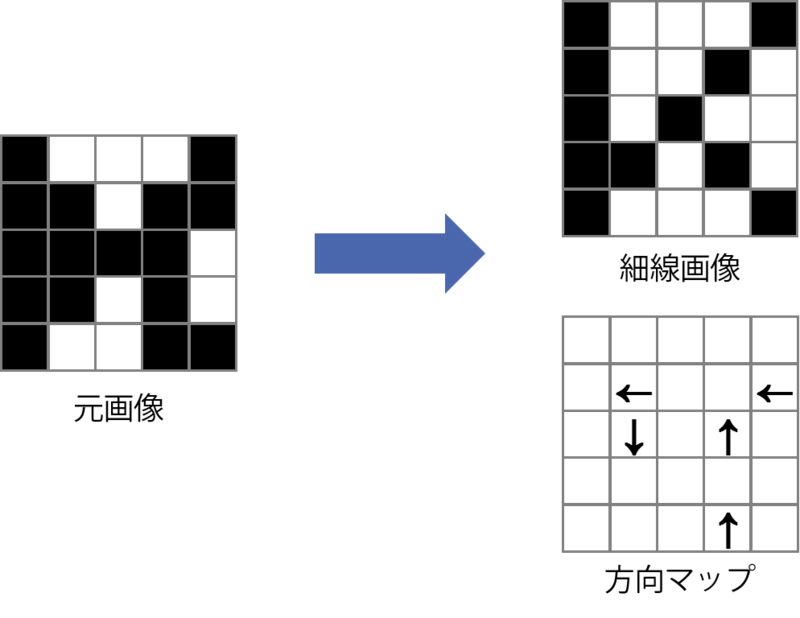
色の伝搬では、色のついた細線画像を基に、方向マップを逆に辿って色を伝搬させます。 実際には、方向マップがより複雑なため、多段階的にこの処理を行うことになります。
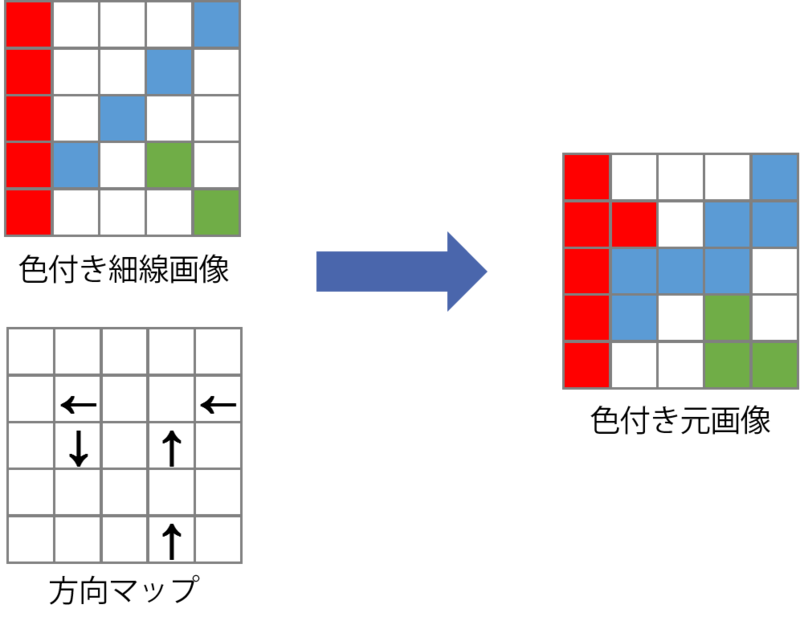
これで元の画像全体に色が割り当てられた状態になり、すべての処理が完了しました。
実装
さて、以上の理論を基に、ここからは実装について書きたいと思います。
言語と環境
HTML・CSS に加えて通常の JavaScript で実装してもいいのですが、 今回は altJS の一つ、TypeScript を採用することにしました。 途中でバージョンアップがあって仕様が変わった部分もありましたが、 明示的な型やクラスなどが使えるので、開発効率は高まったと思います。
最終的には JavaScript に変換される上、DefinitelyTyped を導入すれば JQuery などとも連携できるので、ライブラリを使う上でも問題はありません。
基本処理の実装
TypeScript で画像を画素単位で操作する場合、HTML5 の canvas 要素の context から getImageData を使って画素の行列を得ることができます。 しかし、この行列は各要素にはアクセスできるものの、画像処理を直接行う関数やクラスは用意されていません。 また、そのような処理を行うライブラリもありません。
そこでまずは、この記事の最初で紹介したような基礎的な処理を実装しておくことにしました。 色や点、画像といった基本要素もあらかじめ定義してあります。
グレースケール化
カラーの画像をグレースケールの画像に変換します。 漫画の画像が対象なので基本的には必要ありませんが、カラー画像が入力された場合に備えて先に適用しておきます。
二値化
グレースケール画像を完全な「黒」と完全な「白」の二つの色だけで表現します。 後で出てくるベクタ化の前提になります。

色の反転
二値画像で、黒と白を入れ替えます。 今回は処理の都合で使っている個所があります。

細線化
含まれているすべての線を、幅1画素の線に細くする処理です。 これも、ベクタ化のために必要です。

ベクタ化の実装
ここまで扱っていた画素が集まっているラスタ形式の画像を、ベクタ形式の画像に変換します。 これも比較的単純な処理ですが、新たにベクトルを基本単位とする画像を定義します。
また、ユーザーが描いた線もベクタ画像としてみなすので、canvas 要素においてマウスの移動を取得し、そのときに選択されている色と共に保存します。 canvas 要素で線を描画する場合、アンチエイリアスの切り替えのブラウザ間互換性が十分でないため、描画も自前の画像クラスで行っています。

色割り当ての実装
二段階化
理論では最も重要なアルゴリズムについて説明しましたが、実装にあたってはそのままでは計算が終わらなくなってしまいます。 実装するにあたっては、「最適な色の割り当て」は高速で疎な第1段階と正確で遅い第2段階を組み合わせて用いることで、インタラクティブな動作を実現しています。
第1段階は、最近傍のベクトルを見つけて、同じ色を割り当てる簡単なものです。 単純な手法なので高速ですが、正確さに欠ける場合があります。

第2段階は、理論で説明した方法を用います。 ベクトル同士の類似性で定義された「エネルギー関数」を最小化する問題に落とし込み、さらにグラフ理論の領域である「最小カット問題」に変換します。 つまり、「色の割り当て最適化問題」→「エネルギー関数最小化問題」→「最小カット問題」と問題を変えていくことで、問題を解ける形にしています。
ここでの重要なパラメーターとして、どこまでを第1段階で行うか、というものがあります。 この割合を高めるほど、速度は向上しますが、精度が低下してしまいます。 今回は JavaScript の実行速度を考慮して、精度を犠牲にして速度を確保する方向で調整しています。
3色以上の場合
さらに、3色以上が入力された場合には問題はより複雑になり、NP困難な問題となってしまいます。 理論では触れませんでしたが、この場合には最適な解を求めることはできず、近似的な最適解を求めることで対応することになります。 具体的には、
- すべての色から1色を選び、その色とそれ以外の色で最小カットを求める
- 選んだ色だけのカットを確定する
- 選ばなかった色の中で、1から繰り返す
という操作を繰り返していきます。 このため、色の数の増加に応じて線形に計算回数が増えてしまうという問題が残ります。

最小カット問題の解法
最小カット問題は古くから議論されてきたテーマで、
- Ford-Fulkerson のアルゴリズム
- Edmonds-Karp のアルゴリズム
- Boykov-Kolmogorov のアルゴリズム
など、様々なアルゴリズムが提案されています。 この3手法では、下に行くほど新しく効率的とされますが、複雑になってしまいます。 今回は、Edmonds-Karp のアルゴリズムを採用して、実装が複雑になりすぎず、かつある程度速度を確保できるようにしました。
まとめ
今回は、画像処理をブラウザ上で行う試みについて紹介しました。
画像処理は計算量が大きいものも多いですが、ブラウザの性能も向上し、このようにある程度複雑なものでも気軽に試せるようになっています。 JavaScript では、画像処理を行う試みが少ないだけでなく、やや複雑な理論に基づいた手法を実装しようとするには計算量について考慮する必要があります。 しかし、手軽に使っていただける形にはなったと思うので、普段画像処理に触れることは多くない方も、これを機会に親しみをもってもらえると嬉しいです。